pythonによる機械学習[最尤推定法編]

機械学習

※当記事は、以下の書籍を参考にしてかかせていただきました。

自分の勉強のために気軽に書いているので記述ミスなどあるかもしれません。もし見つけた場合はご連絡ください＞＜

今回は、

palloc.hateblo.jp

の記事で書いたうちの、未来を推測するアルゴリズムの一つである最尤(さいゆう)推定法について理論の説明＆pythonで実装をしてみたいと思います。

上の記事を読んでいることを前提に話を進めるので、読んでいない場合疑問が生じやすいかもしれません。

最尤推定法

最尤推定法とは、確率を用いてデータの特徴変数と目的変数の関数関係を求め、誤差率を出す手法です。

確率を用いた最尤推定の考え方は、他の手法の一部としてよく用いられます。

最小二乗法では、推定した関数から値を予測する際、どれだけの誤差が生まれるかという情報がありませんでした。

そこをカバーできる手法が最尤推定法だというイメージです。

理論

まず、特徴変数をx、目的変数をtとします。

そして、N個のデータ\{x_n,t_n\}_{n=1}^{N}を持っていて、データを分析し新しくxを与えられた時に対応するtを推測するのが目標です。

まず、多項式f(x)を以下のように定義します。

{f(x)=w_{0}+w_{1} x+w_{2} x^{2}+ \cdots +w_{M} x^{M}}

式をまとめると、以下のようになります。

{f(x)=\sum_{m=0}^{M} w_{m} x^{m}\tag{1}}

(1)式の係数を求めるのが最小二乗法でした。

最尤推定法では、「f(x)を中心に観測値はおよそf(x)±σの範囲に存在する」という誤差までを推測します。

とりあえず、正規分布に従う乱数を考えます。

µを中心にµ±σに散らばる乱数は、平均µ、分散{\sigma^{2}}の正規分布で表すことができます。(σは標準偏差として捉えられます。)

正規分布の確率密度関数は、以下のように表されます。

\displaystyle{N(x \;|\; \mu,\sigma^{2})=\frac{1}{\sqrt{2\pi \sigma^{2}}} e^{-\frac{1}{2\sigma^{2}} {(x-\mu)}^{2}}\tag{2}}

確率密度関数とは、一定区間で積分するとその区間が取りうる確率となるような関数です。(詳しくは確率密度関数 - Wikipediaを参考にしてください。)

以下、長いので確率密度関数の事を確率と呼ぶことにします。

今回は、とりあえずf(x)からの観測値のばらつきが正規分布に従っているものとして進めます。(もしも検証結果が良くなければ、別の分布に変えましょう)

f(x)±σの範囲にランダムに観測値tが存在すると仮定し、(2)の式に代入してみます。

\displaystyle{N(t \;|\; f(x_{n}),\sigma^{2})=\frac{1}{\sqrt{2\pi \sigma^{2}}} e^{-\frac{1}{2\sigma^{2}} {\{t-f(x_{n})\}}^{2}}\tag{3}}

ここで、(3)式と(1)式にて、数式のパラメータ、すなわち変数はどれかというと、{{\{w_{m}\}}_{m=0}^{M}}と標準偏差σになります。(x,tは与えられたデータの値です。)

さて、(3)式の意味を考えてみましょう。

(3)式は、確率の式であり、ある特定の{x_{n}}の時の{t_{n}}の際の確率は、(3)のtに代入して、

\displaystyle{N(t_{n} \;|\; f(x_{n}),\sigma^{2})=\frac{1}{\sqrt{2\pi \sigma^{2}}} e^{-\frac{1}{2\sigma^{2}} {\{t_{n}-f(x_{n})\}}^{2}}\tag{4}}

となります。

そして、全てのデータ{{\{x_{n}\}}_{n=1}^{N}}について考えると、学習データ{{\{(x_{n},t_{n})\}}_{n=1}^{N}}そのもの(今持っている学習用データ)が得られる確率は、nが1~Nのときのそれぞれの確率の積です。

この確率Pは、以下のように表すことができます。

{P=N(t_{1}\;|\;f(x_{1}),\sigma^{2})\times \cdots \times N(t_{N}\;|\;f(x_{N}),\sigma^{2})}

これをまとめると、

\displaystyle{P=\prod_{n=1}^{N} N(t_{n}\;|\;f(x_{n}),\sigma^{2})\tag{5}}

となります。

この確率を見ると、パラメーターは(3)式で述べたものと同じです。

この、今持っている学習用データが得られる確率をパラメーターの関数とみなしたものの事を、 尤度関数 と呼びます。

ここで、今得られている学習用データが最も発生確率が高いデータだと仮定して、パラメーターを決定するのが最尤推定法です。

これは、最もエントロピーが少ない状態を想定するというイメージです。

発生確率が最も高いということは、尤度関数が最大になるということですね。

なので、尤度関数Pが最大になる時のパラメータ{{\{w_{m}\}}_{m=0}^{M}}とσを求めましょう。

まず、(5)式に(4)式を代入してみます。

\displaystyle{P=\prod_{n=1}^{N} \frac{1}{\sqrt{2\pi \sigma^{2}}} e^{-\frac{1}{2\sigma^{2}} {\{t_{n}-f(x_{n})\}}^{2}}\tag{6}}

(6)のnが含まれていないところをN乗し、nの含まれているところを指数部の和と捉えることで以下のように変形できます。

\displaystyle{ P=\left(\frac{1}{2\pi \sigma^{2}}\right)^{\frac{N}{2}} e^{-\frac{1}{2\sigma^{2}} \sum_{n=1}^{N}{\{t_{n}-f(x_{n})\}}^{2}}\tag{7} }

(7)式で見ると、最小二乗法の際に求めた二乗誤差Eが含まれていることがわかります。(以下参照)

pythonによる機械学習[概要＆最小二乗法編] - ぱろっくの日記

そこで、二乗誤差Eを(7)式に代入すると、尤度関数Pは以下のようになります。

\displaystyle{ P=\left(\frac{1}{2\pi \sigma^{2}}\right)^{\frac{N}{2}} e^{\frac{1}{\sigma^{2}} E}\tag{8} }

ここで、{\beta=\frac{1}{\sigma^{2}}}とおき、Eのパラメータ{\mathbf{w}=(w_0, \cdots ,w_M)^{T}}とすると、Pは{\beta,\mathbf{w}}がパラメータなので、

\displaystyle{ P(\beta,\mathbf{w})=\left(\frac{\beta}{2\pi}\right)^{\frac{N}{2}} e^{-\beta E(\mathbf{w})}\tag{9} }

とかけます。

ここで、計算をもう少し楽にするために(9)の両辺のlogをとると、以下のようになります。

\displaystyle{ \log P(\beta,\mathbf{w})=\frac{N}{2} \log \beta-\frac{N}{2}\log 2\pi -\beta E(\mathbf{w})\tag{10} }

ちなみに、(10)式を一般的に対数尤度関数と言います。

尤度関数が最大というのと、対数尤度関数が最大なのは等価なので、(10)式を最大化させましょう。

最大になる時、以下の２式が導けます。

\displaystyle{ \frac{\partial \log P}{\partial w_{m}}=0\;\;\;(m=0, \cdots ,M)\tag{11} }

\displaystyle{ \frac{\partial \log P}{\partial \beta}=0\tag{12} }

(11)式に(10)式を代入すると、以下の式が得られます。

\displaystyle{ \frac{\partial E}{\partial w_{m}}=0\tag{13} }

(13)式、これ、どこかで…

そうです、最小二乗法で、誤差を最小にする時の条件式と全く一緒です。

ということで、多項式f(x)の係数{{\{w_{m}\}}_{m=0}^{M}}は、最小二乗法と同じ値になります。

最小二乗法の時と同じく、以下のような式で求められます。

{\mathbf{w}=(\Phi^{T}\Phi)^{-1}\Phi \mathbf{t}}

ちなみに、この関数は最小二乗法問題の正規方程式と呼ばれていて、{\Phi}は計画行列と呼ばれています。

また、(12)式に(10)式を代入して偏微分をすると、以下の式が得られます。

\displaystyle{ \frac{1}{\beta}=\frac{2E}{N}\tag{14} }

(14)式に、{\beta=\frac{1}{\sigma^{2}}}を代入して、σの式が得られます。

\displaystyle{ \sigma=\sqrt{\frac{2E}{N}}\tag{15} }

(15)の二乗誤差Eを展開すると、σは平方平均二乗誤差であることがわかります！(僕はこれを初めて知った時一人で勝手に感動してました。)

さて、以上より、最尤推定法のパラメータが全て定まりました。

なんと、最小二乗法と全く同じ多項式を得てしまいました。

このことから、尤度関数の最大化は、二乗誤差の最小化と等価であることがわかりますね。

なにはともあれ、f(x)とσを定めることができて、目標達成です。

実装

今回は、{f(x)=10(x-0.5)^{2}}という方程式に、標準偏差0.7の正規分布に従う乱数雑音を付加したデータを学習用データとして用意し、最尤推定法によってその式に近い多項式を求め、誤差の範囲を推定するプログラムをpythonで作成しました。使った式に特に意味はありません。

使ったライブラリは、numpy,pandas,matplotlibです。

入ってない方はpipなどで簡単に入れられますので検索してみてください。

学習データ数10,多項式の次数を1,3,5,9でグラフを表示した結果が以下のようになります。

f:id:palloc:20160117174133p:plain

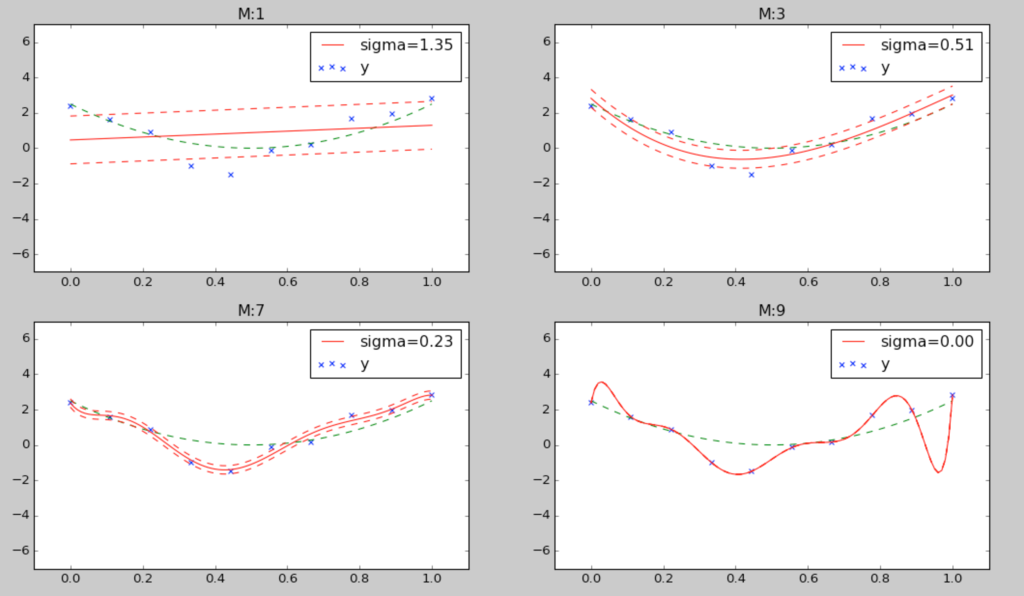
今回は、元の関数がわかりづらいと思ったため緑色の破線で表示しておきました。

まず、多項式を見ると、M=3のときが一番元の式に近いですね。

誤差の範囲も赤の破線で表示しています。

M=9を見てみると、当たり前ですが全ての点を通ってしまっているので誤差なんてありませんね。どう見てもこのデータだけに忠実にフィッティングした過学習状態です。

まとめ

最小二乗法に誤差の情報をプラスしたような結果が得られました。やったね！

最尤推定はとても大切な考え方なので、覚えておくといいことがあるかも。

また、最初に述べた参考書籍には本当にお世話になっております。ありがとうございます！